Write Code that Rates Fairly

Our perception of quality is strongly influenced by internet ratings. We look out for Amazon reviews, movie ratings, how many stars that new game has, the reputation of restaurants in Yelp, or the “coolest” touristic attractions on TripAdvisor. Relying on the wisdom of the masses via online rating systems is a part of our internet culture.

At some point as a programmer, you’re likely to code some type of aggregate rating mechanism yourself. You’ll write the code to rank entities by the average of the ratings given by your users. Once you’re in this position, beware! It’s probably unfair to compare the average rating of entities that have received a very different number of ratings.

Take for example, the movie “A Healthy Baby Girl” and the movie “Titanic”. Both were produced in 1997. Titanic, besides having won 11 Oscars, has an IMDb average rating of 7.8, while the baby movie gets an impressive 8.2. But Titanic was evaluated by over 800 thousand people, while the baby movie received just 28 votes. Now I haven’t seen this baby movie, but it’s questionable that it deserves a higher rating than Titanic. The ratings are probably not fair.

In this post, we’ll discuss three directives you can follow when creating rating mechanisms, to ensure your code is rating things fairly.

Disregard ratings for entities with few voters

The first line of defense against under/over rating is simply not to consider entities that received a number of evaluations below a threshold. For instance, only movies that have received over 25,000 votes are eligible to enter the prestigious “Top 250” movies IMDb list.

But how to decide which threshold to use? If you have a reasonably accurate prior idea of what the true rating of your elements is, you could try filtering your ratings using different thresholds until you notice your ranking is free of grossly wrong ratings.

You can also turn to statistics, and consider the sample size required for a statistically significant survey. Let’s try a ballpark estimate for rating movies. If 50% of adult Americans go to the movies, the number of movie-watchers is around 150 million. Using SurveyMonkey’s “Sample Size Calculator”, it’s easy to see we need several thousand votes for attaining an acceptable level of statistical significance. If you’d like to understand the reasoning behind this, checkout Khan Academy’s confidence interval series.

Some of the IMDb rating data is available for research, so we can plot how the ratings of movies are distributed according to the number of votes. We can see there is a sharp difference in how movies are rated, for movies receiving different number of votes:

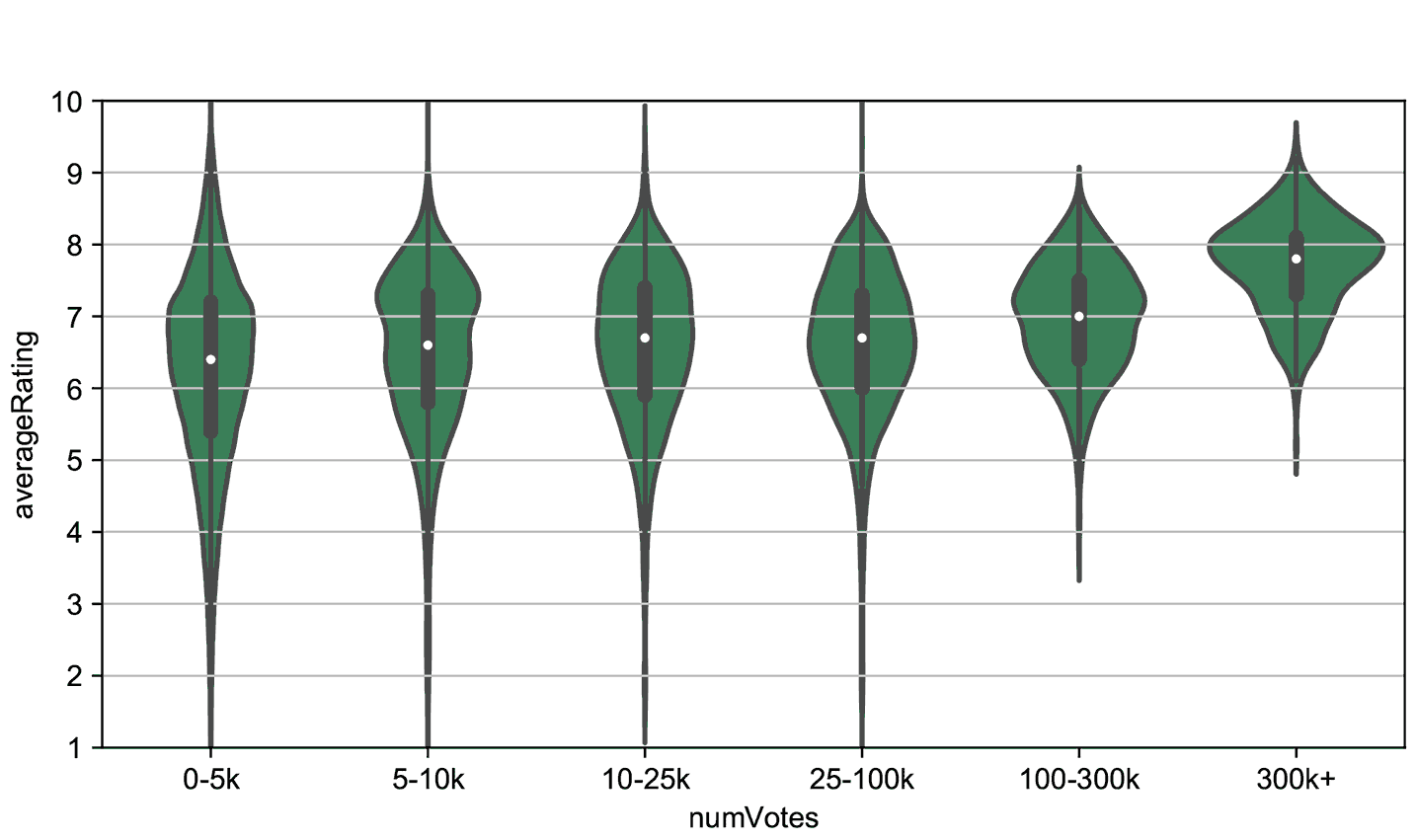
Each “strip” in the graph presents rating data from movies having a number of votes within an interval. For instance, the first strip shows data from movies that received up to 5 thousand votes.

The code required to extract the IMDb data and create this plot is open source, and you can get it from Github. Pull requests are welcome! 😊

Weight ratings according to the number of votes

Even when you consider a statistically relevant sample size, it could still be unfair to compare movies with massive number of ratings to those that barely attain the threshold.

For instance, the movie “The Shape of Water” just won this year’s Oscar’s for Best Picture. This movie has an IMDb average rating of 7.7 with 123 thousand votes. “The Secret of Kells” also received a rating of 7.7, being rated by 26 thousand people. Does that mean both movies are comparable in terms of popular acclaim? I don’t think so…

One way around this problem is to apply a transformation to our average ratings. Our confidence in the average rating is strongly related to the number of ratings received. The more votes, the better we trust that the rating reflects the movie’s actual value. One way to model this idea mathematically is by using a Bayesian Estimator.

This technique was reportedly used by IMDb in the past for their ranking of movies. I won’t delve into the mathematics. For those who are math inclined, there’s a Wikipedia article on Bayes Estimators, and this Fxsolver page for playing around with the formula.

With the Bayes Estimator previously used by IMDb, “The Shape of Water” gets a weighted rating of 7.58, and “The Secret of Kells”, 7.35.

Weight votes according to the voter’s behavior

Even with weighted ratings, we are still susceptible to vote manipulation. For instance, the movie “The Mountain II” has an impressive rating of 9.6, and it was rated by nearly 100 thousand people. Movie critics are nowhere near to acclaiming this movie as a masterpiece. There is an interesting Quora discussion explaining this phenomenon. Probably, many Turkish voters gave the movie a perfect 10 not for its artistic value, but simply because it’s a national blockbuster.

To prevent such manipulation, we need look at each vote individually. It seems IMDb has abandoned the Bayes Estimator, as they removed all references of it from their website. Apparently, they are now more focused on vote weighting. They claim to give more weight to votes of people that appear to vote fairly. They don’t disclose how their system works exactly, so we can’t say much more.

There are several ways individual ratings can be valued more or less, according to the behavior of each voter. For instance, the photo-ranking site Photofeeler gives a stronger weight for a high vote coming from someone who generally rates below the site’s average.

Conclusion

It’s very tricky to use loose, aggregate ratings from diverse people on the internet to accurately rank things. If you are the one behind such a system, it’s your responsibility to properly analyze your data, not to present your users with misleading ratings.

Related articles

• Al Gore’s New Movie Exposes The Big Flaw In Online Movie Ratings
• How rateyourmusic.com weights users’ votes to prevent abuse
• I Made My Shed the Top Rated Restaurant On TripAdvisor

Have you created a rating system yourself? Which measures did you take to ensure your ratings were accurate? Let us know in the comments below!